Renovation - Kitchen Ceiling

 

Recently, I completed a renovation

of the kitchen ceiling,

where I am living.

My landlady is directing 

the renovations,

they are her creative ideas,

and she is supplying 

the equipment and materials.

Here, you can see,

  -  the prepared surface

  -  the painted trim

  -  the completed ceiling

The paint is a gloss black,

and has a very warm and soft look

at night, with the yellowish light globe 

turned on.

(c) Katherine Stuart 2020

Dochas Books Film

Basic Graphics #8 - Wave

 

8.  WAVE

WAVE  #1

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>> def SquareArcAC(radius):

         n = radius/57.35

         a = n/2

         for i in range(4):

              Pt.forward(radius)

              Pt.left(90)

         Pt.forward(a)

         Pt.left(1)

         for i in range(89):

              Pt.forward(n)

              Pt.left(1)

         Pt.forward(a)

>>> def SquareArcC(radius):

         n = radius/57.35

         a = n/2

         for i in range(4):

              Pt.forward(radius)

              Pt.right(90)

         Pt.forward(a)

         Pt.right(1)

         for i in range(89):

              Pt.forward(n)

              Pt.right(1)

         Pt.forward(a)

 

>>>

>>> Pt.backward(200)

>>> Pt.right(90)

>>>

>>> SquareArcAC(100)

>>> SquareArcAC(100)

>>>

>>> SquareArcC(100)

>>> SquareArcC(100)

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

TILES

The tiles used here, are –

            SquareArcAC(radius)

            Square  Arc  Anti-Clockwise

            Which turns to the    left

 

            SquareArcC(radius)

            Square  Arc  Clockwise

            Which turns to the    right

 

POSITION

Firstly,

The  Pt  has been positioned,

so that the wave will end up being centred in the screen.

 

ARRANGEMENT

Two anti-clockwise Square Arcs,

are followed by,

two clockwise Square Arcs.

 

This arrangement produces,

the    Wave    mechanism.

We can simplify the    Wave    mechanism,

in  Wave  #2 -

WAVE  #2

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>> def SquareArcAC(radius):

         n = radius/57.35

         a = n/2

         for i in range(4):

              Pt.forward(radius)

              Pt.left(90)

         Pt.forward(a)

         Pt.left(1)

         for i in range(89):

              Pt.forward(n)

              Pt.left(1)

         Pt.forward(a)

>>> def SquareArcC(radius):

         n = radius/57.35

         a = n/2

         for i in range(4):

              Pt.forward(radius)

              Pt.right(90)

         Pt.forward(a)

         Pt.right(1)

         for i in range(89):

              Pt.forward(n)

              Pt.right(1)

         Pt.forward(a)

 >>> def Wave(radius):

         for i in range(2):

             SquareArcAC(radius)

         for i in range(2):

             SquareArcC(radius)

 

         

>>>

>>> Pt.backward(200)

>>> Pt.right(90)

>>>

>>> Wave(100)

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

 

For a Wave of any size,

we introduced, into the mechanism,

the variable -

            radius

 

Here, 

 

radius  =  number of pixels distance,

                from the centre of the rotation, 

                to its arc,

                which is also the length of the side of the square,

                in the SquareArc tiles

SquareArcAC(radius)    and    

SquareArcC(radius)

need to have  radius  inside them.

 

This is because, they are inside 

Wave(radius),

and this syncs them with

Wave(radius).

              

 

Then,

all we have to do,

to draw a wave of a certain size,

is write the  Wave(radius)  mechanism, in the program,

and put in the size of the radius that we want, for example -

           

Wave(100)

(c) Katherine Stuart 2020

Dochas Books Film

Basic Graphics #7 - Scroll

7.  SCROLL

SCROLL  #1

 

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>> def SquareArc(radius):

     n = radius/57.35

     a = n/2

     for i in range(4):

          Pt.forward(radius)

          Pt.right(90)

     Pt.forward(a)

     Pt.right(1)

     for i in range(89):

          Pt.forward(n)

          Pt.right(1)

     Pt.forward(a) 

>>>

>>> Pt.forward(50)

>>> Pt.right(90)

>>>

>>> SquareArc(50)

>>> SquareArc(50)

>>>

>>> SquareArc(100)

>>> SquareArc(100)

>>>

>>> SquareArc(150)

>>> SquareArc(150)

>>>

>>> SquareArc(200)

>>> SquareArc(200)

>>>

>>>

>>> turtle.done()

>>> 

SAVE

Firstly,

the Pt has been positioned where the first arc will eventually start.

Then,

2 SquareArcs have been drawn with the initial radius of    50,

And then,

2 SquareArcs have been drawn with the increased radius of    + 50,

And so on.

 

This arrangement of the SquareArcs produces the Scroll pattern.

VARIABLES

 

 

Variables are amounts, in the program, which can change / vary.

 

Number of pixels, and,

Number of degrees,

are variables.

 

We can write variables into items in the program, within the parentheses    ( )    ,

as in the generalised versions of the previous programs.

Where, they will only apply to the item that they are attached to, such as –

 

Pt.forward(number of pixels)

Pt.right(number of degrees)

  

We can also write the variables into the name of a mechanism,

within the parentheses    ( )    .

But, then they will apply to the whole mechanism, such as –

 

SquareArc(radius)

 

Here, the variable is -

            radius

  

Using variables, we can simplify  Scroll  #1, into  Scroll  #2, below -

SCROLL  #2

 

 

SAVE AS

>>> import turtle

>>>

>>> def SquareArc(radius):

     n = radius/57.35

     a = n/2

     for i in range(4):

          Pt.forward(radius)

          Pt.right(90)

     Pt.forward(a)

     Pt.right(1)

     for i in range(89):

          Pt.forward(n)

          Pt.right(1)

     Pt.forward(a)

>>> def Scroll(radius, radius_increase, t):

      nht = 2*t

      for i in range(nht):

          for i in range(2):

              SquareArc(radius)

          radius = radius + radius_increase

         

>>>

>>> Pt.forward(50)

>>> Pt.right(90)

>>>

>>> Scroll(50, 50, 2)

>>>

>>>

>>> turtle.done()

>>>

SAVE

TILE

The SquareArc  can be called a  “tile”,

in that, all the elements within it are connected,

and it can move as one unit.

 

ARRANGEMENT

This arrangement of the SquareArcs,

using the mechanism -

            Scroll(radius, radius_increase, t)

produces the Scroll pattern.

 

 

Here, in Scroll(radius, radius_increase, t),

radius  =  same radius as in SquareArc(radius)

radius_increase  =  increase in the radius after drawing each set of 2 SquareArcs

                               (The bottom bar _  joins the two words, so that the computer knows it is

                                one item, not two)

t  =  number of complete turns / cycles of the scroll that is required

nht  =  number of half turns of the scroll,

            which is the number of sets of  2  SquareArcs

 

Firstly,

the Pt has been positioned where the first arc will eventually start.

 

For,

Each turn / cycle needed of the scroll,

there needs to be -

            2  x  t    half turns / sets of  2  SquareArcs 

 

But,

after each set is completed,

there needs to be an increase in the radius,

to make the next set larger.

This is achieved by using the equation –

            (outside the “for” loop for the set of  2  SquareArcs,

            by tabbing it backwards in line with the beginning of that loop)

  

            radius  =  radius  +  radius_increase

           

            The computer can understand this type of equation, as saying –

 

                        new radius  =  previous radius  +  radius_increase

 

            In this mechanism, the radius increases by its original amount, each time,

            which is said to be a  “regular”  increase -  that is, “the same” increase each time.

(c) Katherine Stuart 2020

Dochas Books Film

Poem - "Gyps - e"

 

"Gyps  -  e"

For Jimmy and Jane

Gyps - e, Gyps - e,

What a pretty name,

Gyps - e, Gyps - e,

I would like the same.

How I miss, to feel the joy,

More than just, a little toy,

Strumming fingers all the while,

Humming tunes that make me smile.

Gyps - e, Gyps - e,

Don't forget your name,

Gyps - e, Gyps - e,

Life without you's not the same.

text (c) Katherine Stuart 2020

Dochas Books Film

Basic Graphics #6 - Arc

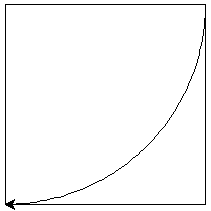
6.  ARC

 

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>> n = 200/57.35

>>> a = n/2

>>>

>>> def Square():

       for i in range(4):

           Pt.forward(200)

           Pt.right(90)

 

         

>>> def Arc():

       Pt.forward(a)

       Pt.right(1)

       for i in range(89):

           Pt.forward(n)

           Pt.right(1)

       Pt.forward(a)

>>>

>>> Square()

>>>

>>> Pt.forward(200)

>>> Pt.right(90)

>>>

>>> Arc()

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

 

This arc mechanism

turns    CLOCKWISE

For any arc

n = radius/57.35

a = n/2

 

def Arc():

   Pt.forward(a)

   Pt.right(1)

   for i in range(number    

   of degrees - 1):

       Pt.forward(n)

       Pt.right(1)

   Pt.forward(a)

 

 

57.35    is the number that gives a correct proportion for the chord, n, 

subtending 1° in this python shell, 

because of the way the point moves in the deeper levels of the program. 

See maths theory for the meaning of “subtending”, and, 

1° turn outside of circle = 1° turn at centre of circle.

Note: If this number doesn't work on your python shell,

just tweak it until the circle moves exactly on top of all four intercepts 

with the four quadrant square. (See below)

MAKING THE ARC

 

 

This involves understanding,

how to move the point.

It is very difficult to move the point

in an actual arc.

So, the point is moved in a series of chords, which are -

 

n    pixels in length

1    degree to the right

        a small enough change for your eye

        not to see the small chords, but,

        interpret them as an arc

a    is half of    n

        use once at the start

        and once at the end of the arc    

        to centre the chords at those points

        2  x  a    is one chord

USING MATHEMATICAL EQUATIONS

 

 

Mathematical equations can be used in computer programs.

 

Here, these equations are being used –

 

n = 200/57.35

a = n/2

 

+     plus

-      minus

*     multiply

/      divide

( )    parentheses

 

They can be written in anywhere in the program.

But, keep in mind, that the computer will not understand it, 

unless it is placed BEFORE it needs to be used.

  

In –

ARC    &    CIRCLE

 

The equations have been written near the beginning of the program.

And, the computer will use them for the whole program.

 

In –

SQUARE-ARC    &    GRID-CIRCLE

 

The equations have been written into the mechanisms, themselves,

SquareArc()    &    GridCircle()

And, the computer will only use the equations for the mechanism that they are in.

 

THE CIRCLE

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>> n = 200/57.35

>>> a = n/2

>>>

>>> def Grid():

     for i in range(4):

         for i in range(4):

             Pt.forward(200)

             Pt.right(90)

         Pt.right(90)

 

          

>>> def Circle():

     Pt.forward(a)

     Pt.right(1)

     for i in range(359):

         Pt.forward(n)

         Pt.right(1)

     Pt.forward(a)

 

    

>>>

>>> Grid()

>>>

>>> Pt.forward(200)

>>> Pt.right(90)

>>>

>>> Circle()

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

 

Grid()

This is the Four Squares mechanism –

def Grid():

   for i in range(4):

       for i in range(4):           

           Pt.forward(number 

           of pixels)

           Pt.right(90)

       Pt.right(90)

 

Circle()

This is the arc mechanism using,

(360  -  1)    degrees -

n = radius/57.35

a = n/2

def Circle():

    Pt.forward(a)

    Pt.right(1)

    for i in range(359):

        Pt.forward(n)

        Pt.right(1)

    Pt.forward(a)

SQUARE-ARC 

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>>

>>> def SquareArc():

       n = 200/57.35

       a = n/2

       for i in range(5):

           Pt.forward(200)

           Pt.right(90)

       Pt.forward(a)

       Pt.right(1)

       for i in range(89):

           Pt.forward(n)

           Pt.right(1)

       Pt.forward(a)

>>> 

>>> SquareArc()

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

Joining the Square() mechanism and the Arc() mechanism -

def SquareArc():

   n = radius/57.35

   a = n/2

   for i in range(5):

       Pt.forward(number of

       pixels)

       Pt.right(90)

   Pt.forward(a)

   Pt.right(1)

   for i in range(89):

       Pt.forward(n)

       Pt.right(1)

   Pt.forward(a)

GRID-CIRCLE

 

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>>

>>> def GridCircle():

     n = 200/57.35

     a = n/2

     for i in range(4):

         for i in range(4):

             Pt.forward(200)

             Pt.right(90)

         Pt.right(90)

     Pt.forward(200)

     Pt.right(90)

     Pt.forward(a)

     Pt.right(1)

     for i in range(359):

         Pt.forward(n)

         Pt.right(1)

     Pt.forward(a)

 

    

>>>

>>> GridCircle()

>>>

>>> 

>>> turtle.done()

>>> 

SAVE

 

 

Joining the Grid() mechanism and the Circle() mechanism -

def GridCircle():

   n = radius/57.35

   a = n/2

   for i in range(4):

       for i in range(4):  

           Pt.forward(number

           of pixels)

           Pt.right(90)

       Pt.right(90)

   Pt.forward(number of

   pixels)

   Pt.right(90)

   Pt.forward(a)

   Pt.right(1)

   for i in range(359):

       Pt.forward(n)

       Pt.right(1)

   Pt.forward(a)

(c) Katherine Stuart 2020

Dochas Books Film