Basic Graphics #6 - Arc

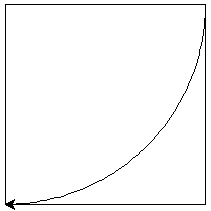
6.  ARC

 

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>> n = 200/57.35

>>> a = n/2

>>>

>>> def Square():

       for i in range(4):

           Pt.forward(200)

           Pt.right(90)

 

         

>>> def Arc():

       Pt.forward(a)

       Pt.right(1)

       for i in range(89):

           Pt.forward(n)

           Pt.right(1)

       Pt.forward(a)

>>>

>>> Square()

>>>

>>> Pt.forward(200)

>>> Pt.right(90)

>>>

>>> Arc()

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

 

This arc mechanism

turns    CLOCKWISE

For any arc

n = radius/57.35

a = n/2

 

def Arc():

   Pt.forward(a)

   Pt.right(1)

   for i in range(number    

   of degrees - 1):

       Pt.forward(n)

       Pt.right(1)

   Pt.forward(a)

 

 

57.35    is the number that gives a correct proportion for the chord, n, 

subtending 1° in this python shell, 

because of the way the point moves in the deeper levels of the program. 

See maths theory for the meaning of “subtending”, and, 

1° turn outside of circle = 1° turn at centre of circle.

Note: If this number doesn't work on your python shell,

just tweak it until the circle moves exactly on top of all four intercepts 

with the four quadrant square. (See below)

MAKING THE ARC

 

 

This involves understanding,

how to move the point.

It is very difficult to move the point

in an actual arc.

So, the point is moved in a series of chords, which are -

 

n    pixels in length

1    degree to the right

        a small enough change for your eye

        not to see the small chords, but,

        interpret them as an arc

a    is half of    n

        use once at the start

        and once at the end of the arc    

        to centre the chords at those points

        2  x  a    is one chord

USING MATHEMATICAL EQUATIONS

 

 

Mathematical equations can be used in computer programs.

 

Here, these equations are being used –

 

n = 200/57.35

a = n/2

 

+     plus

-      minus

*     multiply

/      divide

( )    parentheses

 

They can be written in anywhere in the program.

But, keep in mind, that the computer will not understand it, 

unless it is placed BEFORE it needs to be used.

  

In –

ARC    &    CIRCLE

 

The equations have been written near the beginning of the program.

And, the computer will use them for the whole program.

 

In –

SQUARE-ARC    &    GRID-CIRCLE

 

The equations have been written into the mechanisms, themselves,

SquareArc()    &    GridCircle()

And, the computer will only use the equations for the mechanism that they are in.

 

THE CIRCLE

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>> n = 200/57.35

>>> a = n/2

>>>

>>> def Grid():

     for i in range(4):

         for i in range(4):

             Pt.forward(200)

             Pt.right(90)

         Pt.right(90)

 

          

>>> def Circle():

     Pt.forward(a)

     Pt.right(1)

     for i in range(359):

         Pt.forward(n)

         Pt.right(1)

     Pt.forward(a)

 

    

>>>

>>> Grid()

>>>

>>> Pt.forward(200)

>>> Pt.right(90)

>>>

>>> Circle()

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

 

Grid()

This is the Four Squares mechanism –

def Grid():

   for i in range(4):

       for i in range(4):           

           Pt.forward(number 

           of pixels)

           Pt.right(90)

       Pt.right(90)

 

Circle()

This is the arc mechanism using,

(360  -  1)    degrees -

n = radius/57.35

a = n/2

def Circle():

    Pt.forward(a)

    Pt.right(1)

    for i in range(359):

        Pt.forward(n)

        Pt.right(1)

    Pt.forward(a)

SQUARE-ARC 

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>>

>>> def SquareArc():

       n = 200/57.35

       a = n/2

       for i in range(5):

           Pt.forward(200)

           Pt.right(90)

       Pt.forward(a)

       Pt.right(1)

       for i in range(89):

           Pt.forward(n)

           Pt.right(1)

       Pt.forward(a)

>>> 

>>> SquareArc()

>>>

>>>

>>> turtle.done()

>>> 

SAVE

 

Joining the Square() mechanism and the Arc() mechanism -

def SquareArc():

   n = radius/57.35

   a = n/2

   for i in range(5):

       Pt.forward(number of

       pixels)

       Pt.right(90)

   Pt.forward(a)

   Pt.right(1)

   for i in range(89):

       Pt.forward(n)

       Pt.right(1)

   Pt.forward(a)

GRID-CIRCLE

 

 

SAVE AS

>>> import turtle

>>>

>>> Pt = turtle.Turtle()

>>>

>>>

>>> def GridCircle():

     n = 200/57.35

     a = n/2

     for i in range(4):

         for i in range(4):

             Pt.forward(200)

             Pt.right(90)

         Pt.right(90)

     Pt.forward(200)

     Pt.right(90)

     Pt.forward(a)

     Pt.right(1)

     for i in range(359):

         Pt.forward(n)

         Pt.right(1)

     Pt.forward(a)

 

    

>>>

>>> GridCircle()

>>>

>>> 

>>> turtle.done()

>>> 

SAVE

 

 

Joining the Grid() mechanism and the Circle() mechanism -

def GridCircle():

   n = radius/57.35

   a = n/2

   for i in range(4):

       for i in range(4):  

           Pt.forward(number

           of pixels)

           Pt.right(90)

       Pt.right(90)

   Pt.forward(number of

   pixels)

   Pt.right(90)

   Pt.forward(a)

   Pt.right(1)

   for i in range(359):

       Pt.forward(n)

       Pt.right(1)

   Pt.forward(a)

(c) Katherine Stuart 2020

Dochas Books Film